Math and Art – Functions Properties

Mathematics lessons must meet the needs of students’ personality development by stimulating capacities, skills and attitudes based on critical, logical, divergent and creative thinking. To achieve these, attractive and engaging mathematics lessons need to be taught using modern student-centred methods. Transforming a lesson in an agile way using the ACCED toolkit brings these benefits.

Non-violent communication is used in group work and in the warm-up activity, where students are asked to choose a mood that helps to relax the atmosphere. Moreover, the interpretation of these drawings makes the transition to the contents to be updated and applied. These activities help students to approach mathematics with love and without fear, to discover their skills for this object. 

The Agile/Scrum strategy is used in Team cooperation, also in each sprint, where tasks are related to the definition of done.

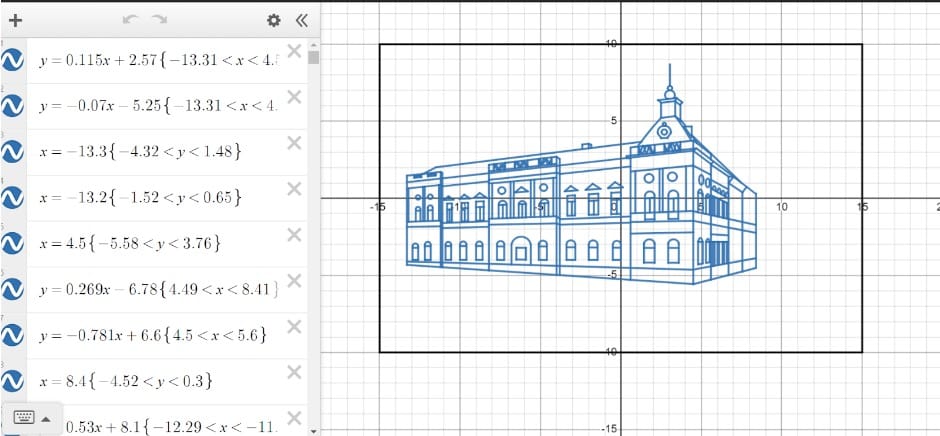
In Sprint 1 the teacher makes a short revision of function properties (parity, monotony, convexity, intersection with axes) and presents them the Desmos Graphing Calculator. Integrating technology to this lesson develops the students ability to use resources (computers, Desmos, Miro, internet) for learning activities and allows the diversification of teaching strategies. Also, the graphical representation of the functions represents an useful intuitive support in studying their properties.

 In Sprint 2  instead of the teacher presenting the students the properties of the four types of functions, the students are challenged to discover them in working groups by interpreting the graphs of the functions. In a group, students work according to the 1-2-4-All Liberating structure. Each  of the four groups studies a type of function and then presents them to their colleagues.

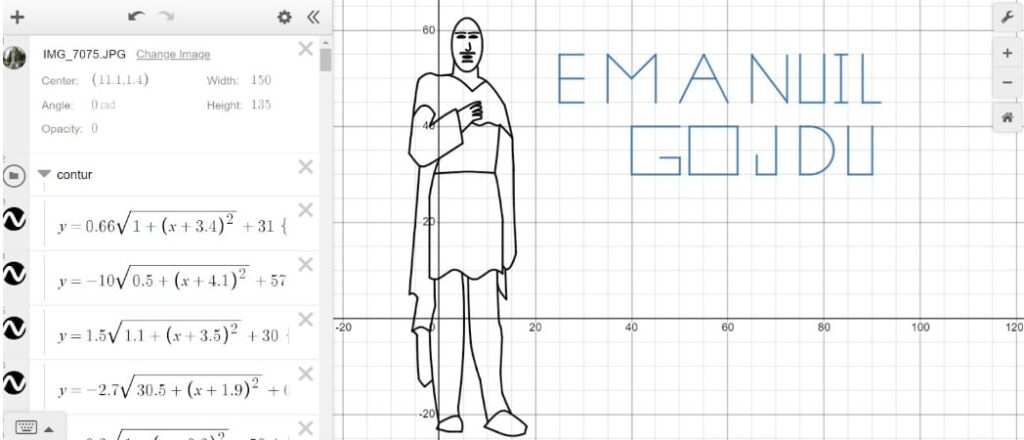
PBL (project-based learning) is used in Sprint 3 to carry out the assessment. Students are asked to make a drawing related to a given topic, using at least fifty lines representing graphs of some studied functions. Completion of this project involves the comparative application of the properties of the functions, giving the student the opportunity to learn in a pleasant way.